The Process
Reading the paper and making the decomposition
Our first week was spent on giving a thorough reading of the paper and understanding how the algorithm works. At the same time, we were also trying to understand the implementation of the DCEL data structure.
It goes without saying that our first model of the DCEL implementation was not all perfect. It was a culmination of consistent testing and adaptation. Eventually we reached a point where we could then focus on coding the given algorithm. We divided the algorithm into the following parts :
- Making the path vector at every iteration
- Make the lpvs vector
- Backtracking phase
- Recursively calling all these parts inside a single function
Testing the Decomposition algorithm
We gathered test cases from various sources in the internet with greater than 15 vertices in each output and plotted a graph of the input data. We then manually implemented the algorithm using pen and paper for some of the test cases that were not so complex, ran the decomposition algorithm on the data simultaneously to get the output plot, and checked the output plot with our manual graph plot to verify it is correct or not. For the complex test cases, we just plotted the output plot by the algorithm and then verified if all the angles present inside the decomposed polygons are not reflex.
Merging the redundant decomposed polygons using the Merging algorithm
We created the lists mentioned in the Merging algorithm (LLE, LP, LUP, LDP) and then worked on it step by step. Now, using the test cases that we had gathered, we ran the algorithm on the input test cases we had used for Decomposition algorithm, and compared the two outputs. For some inputs, the merging algorithm reduced the number of polygons present in the first output as redundant decompositions were merged to give minimum number of decomposition possible, while for other inputs, since the polygon had no redundant decompositions, the two outputs were the same.
Time Analysis
The Following Functions are being Called:
DecomposeDCEL():
Finding Longest Path Takes O(n) time
MakeDCEL Takes O(n) time
Let Maximum Edges = t (=n)
Creating LPVS Takes O(n) time
For all the vertices, check if it is inside the polygon or not
This function takes O(n)*O(t) time
Since we run this n time(popping a point if it is inside and checkinagain), it becomes O(n^3)
Now, we recursively Call `DecomposeDCEL()` function
=> T(n) = O(n*3) + T(n-p)
Overall Time Complexity: O(n^3)
InitLP() takes O(n^2)
Merging():
For every diagonal(n diagonals):
`Next()` takes O(n)
Traversing Through LP takes O(n)
`MergePolygon()` takes O(n)
=>So overall time complexity: O(n^2)
For the entire algorithm, time complexity: O(n^3) + O(n^2) = O(n^3)
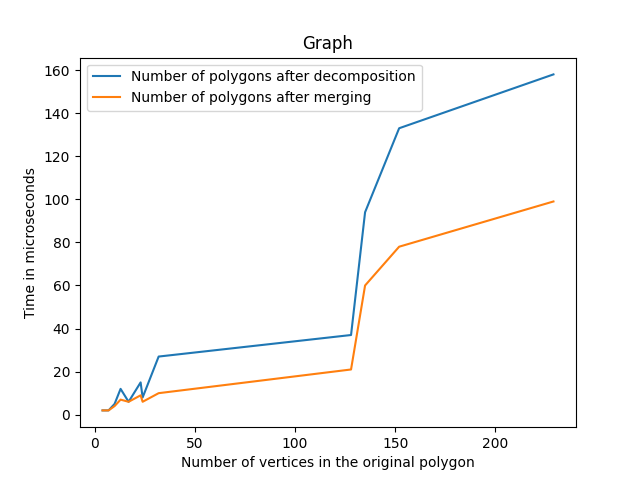
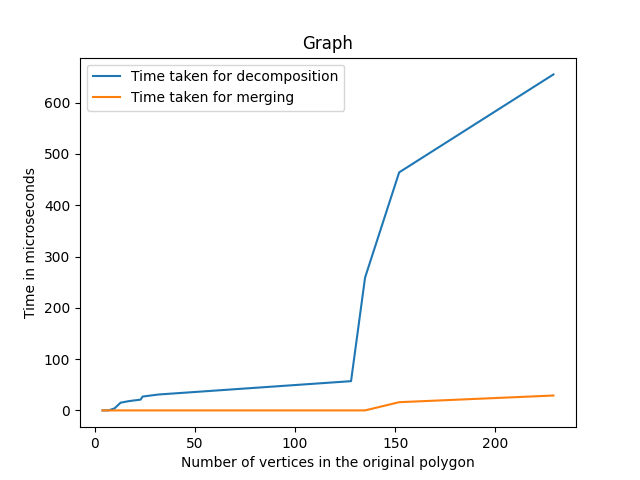
Results
| Input Size | Number of Polygons after decomposition | Time taken for decomposition | Number of Polygons after merging | Time taken for merging |
|---|---|---|---|---|
| 4 | 2 | 0ms | 2 | 0ms |
| 7 | 2 | 0ms | 2 | 0ms |
| 10 | 5 | 0.004ms | 4 | 0ms |
| 13 | 12 | 0.015ms | 7 | 0ms |
| 17 | 6 | 0.018ms | 6 | 0ms |
| 23 | 15 | 0.021ms | 9 | 0ms |
| 24 | 8 | 0.027ms | 6 | 0ms |
| 32 | 27 | 0.031ms | 10 | 0ms |
| 128 | 37 | 0.057ms | 21 | 0ms |
| 135 | 94 | 0.259ms | 60 | 0ms |
| 152 | 133 | 0.464ms | 78 | 0.016ms |
| 229 | 158 | 0.655ms | 99 | 0.029ms |
Note that 0ms means that the time taken is so small it can't even be represented in double data type.
Plots